반응형
행렬 기초 및 벡터 변환 가이드 (고1 선택)
고등학교 1학년 선택 과목으로 배우는 행렬(matrix) 은 여러 벡터를 한 번에 다루거나, 연립방정식·좌표변환·컴퓨터 그래픽 등 다양한 분야에 활용되는 강력한 도구입니다.

이 글에서는
- 행렬의 정의와 기본 연산
- 행렬과 벡터의 곱을 통한 벡터 변환
- 직교 변환·확대·회전·반사 매트릭스
- 실전 예제와 팁
을 차례로 정리하여, 행렬과 벡터 변환의 핵심 개념을 이해하고 실전에 바로 적용할 수 있도록 안내합니다.
행렬의 기초
행렬의 정의
- $m\times n$ 행렬이란, 가로 $n$개, 세로 $m$개 숫자를 직사각형 배열로 놓은 것
- 보통 대문자 $A=[a_{ij}]$로 표기하며, $a_{ij}$는 $i$번째 행, $j$번째 열 원소
행렬 덧셈·스칼라배
- 덧셈: 같은 크기의 행렬 $A,B$에 대하여
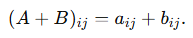
- 스칼라배: 수 $c$와 행렬 $A$에 대하여

행렬 곱셈
- $A$는 $m\times p$, $B$는 $p\times n$ 행렬일 때,
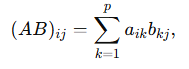
결과는 $m\times n$ 행렬
- 주의: 곱셈은 교환법칙이 성립하지 않음 ($AB\neq BA$ 일반적)
전치행렬
- $A^T$는 $A$의 행과 열을 뒤집은 행렬: $(A^T){ij}=a{ji}$
- 회전·직교 성질 해석에 활용
벡터 변환과 행렬
벡터를 행렬로 표현
- 2차원 벡터 $\mathbf{v}=(x,y)$는 열벡터로

- 행렬 $A$와 곱하면 새로운 벡터로 변환
행렬 곱을 통한 변환
- $A$가 $2\times2$, $\mathbf{v}$가 $2\times1$일 때

- 행렬은 벡터의 선형 변환(linear transformation) 을 나타냄
기본 변환 매트릭스
단위행렬(Identity)

- 곱해도 벡터가 변하지 않음
확대·축소 스케일링

- $x$-축 방향 $k_x$배, $y$-축 방향 $k_y$배 변환
회전 변환
- 각도 $\theta$만큼 시계 반대 방향 회전
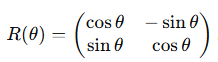
반사 변환

전단(shear) 변환

- 기하 왜곡 효과
복합 변환과 행렬 곱
합성 변환
- 두 변환 $A,B$를 연속 적용하려면 행렬 곱 $B,A$
- 순서 중요: $B(A\mathbf{v})\neq A(B\mathbf{v})$
역변환
- 정방행렬 $A$ 중 역행렬 $A^{-1}$가 존재하면
$$
A^{-1}A = AA^{-1} = I
$$
- 변환을 원래대로 돌리고 싶을 때 사용
실전 예제
예제 1: 회전 후 확대
- 점 $(1,0)$을 45° 회전한 뒤 $x$, $y$축 각각 2배 확대
- 계산:

예제 2: 회전·반사 합성
- 90° 회전 후 $y$-축 반사하려면
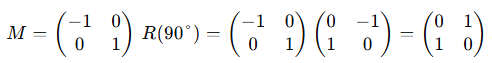
- 결과는 $x,y$ 축 교환
응용 팁
- 행렬의 곱셈 순서 확인: 오른쪽 행렬이 먼저 적용
- 단위행렬로 변환 검산: 복합 변환 후 역변환 곱해 $I$ 확인
- 전치행렬은 회전·반사의 역변환과 같다($R^{-1}=R^T$)
결론
- 행렬 기초: 덧셈·스칼라배·곱셈·역행렬
- 벡터 변환: 선형 변환을 행렬 곱으로 표현
- 주요 매트릭스: 단위·스케일·회전·반사·전단
- 합성·역변환: 변환 순서와 역행렬
행렬과 벡터 변환의 원리를 이해하면, 좌표 변화·도형 변환·컴퓨터 그래픽 등 다양한 분야에서 응용할 수 있습니다. 오늘 정리한 예제와 공식을 바탕으로, 직접 여러 복합 변환을 연습해 보시기 바랍니다.
반응형
'과학 생물 천체 공학 수학 > mathematics' 카테고리의 다른 글
| 삼각형 중선·무게중심·외심·내심 벡터 풀이 (0) | 2025.05.29 |
|---|---|
| 원·타원·쌍곡선·포물선의 초점 기법 (0) | 2025.05.27 |
| 구면·원뿔·원통의 단면 기하 (0) | 2025.05.21 |
| 벡터를 활용한 삼각형 면적 및 사면체 체적 계산 가이드 (0) | 2025.05.18 |
| 직선·평면 방정식 총망라 (0) | 2025.05.16 |



