공간벡터 및 3차원 좌표 기본
공간벡터와 3차원 좌표계는 공학·물리·컴퓨터 그래픽 등 다양한 분야에서 필수적인 도구입니다. 2차원 평면벡터에서 습득한 개념을 확장해, 3차원 공간에서의 위치·방향·면·직선 등 복잡한 기하 구조를 벡터로 깔끔하게 해석할 수 있습니다.

이 글에서는
- 3차원 직교좌표계와 벡터 표현
- 공간벡터의 덧셈·스칼라배·내적·외적
- 벡터 방정식으로 직선·평면 표현
- 거리·면적·체적 계산 기초
를 차례대로 살펴보고, 실전 문제 풀이 팁을 드리겠습니다.
3차원 직교좌표계와 벡터 표현
좌표축과 기저벡터
3차원 공간에서는 서로 수직인 세 축을 설정합니다.
- $x$축: 단위벡터 $\mathbf{i}=(1,0,0)$
- $y$축: 단위벡터 $\mathbf{j}=(0,1,0)$
- $z$축: 단위벡터 $\mathbf{k}=(0,0,1)$
이 세 단위벡터를 표준기저(standard basis) 라 부르며, 임의의 점 $P(x,y,z)$는
$$
\overrightarrow{OP} = x,\mathbf{i} + y,\mathbf{j} + z,\mathbf{k}.
$$
벡터의 좌표 표현
공간벡터 $\mathbf{v}$를 성분으로 나타낼 때는
$$
\mathbf{v} = \langle v_x,,v_y,,v_z\rangle
$$
또는
$$
\mathbf{v} = v_x,\mathbf{i} + v_y,\mathbf{j} + v_z,\mathbf{k}.
$$
공간벡터의 연산
벡터 덧셈 및 스칼라 배
- 덧셈:
$\mathbf{u} = \langle u_x,u_y,u_z\rangle$,
$\mathbf{v} = \langle v_x,v_y,v_z\rangle$일 때 - $$
\mathbf{u} + \mathbf{v} = \langle u_x+v_x,;u_y+v_y,;u_z+v_z\rangle.
$$ - 스칼라배:
상수 $c$에 대한 - $$
c,\mathbf{v} = \langle c,v_x,;c,v_y,;c,v_z\rangle.
$$
벡터의 크기(norm)
$$
|\mathbf{v}| = \sqrt{v_x^2 + v_y^2 + v_z^2}.
$$
내적(dot product)
$$
\mathbf{u}\cdot\mathbf{v} = u_xv_x + u_yv_y + u_zv_z
= |\mathbf{u}||\mathbf{v}|\cos\theta.
$$
- 직교 판정: $\mathbf{u}\cdot\mathbf{v}=0$ 이면 수직
외적(cross product)
$$
\mathbf{u}\times\mathbf{v}
= \langle u_yv_z - u_zv_y,;u_zv_x - u_xv_z,;u_xv_y - u_yv_x\rangle.
$$
- 결과는 두 벡터에 모두 수직인 벡터
- 크기 $|\mathbf{u}\times\mathbf{v}| = |\mathbf{u}||\mathbf{v}|\sin\theta$
벡터 방정식으로 직선·평면 표현
직선의 벡터 방정식
점 $\mathbf{r}_0$에서 방향벡터 $\mathbf{d}$로 뻗는 직선
$$
\mathbf{r}(t) = \mathbf{r}_0 + t,\mathbf{d},\quad t\in\mathbb{R}.
$$
평면의 벡터 방정식
점 $\mathbf{r}_0$과 법선벡터 $\mathbf{n}$이 주어질 때 평면
$$
\mathbf{n}\cdot(\mathbf{r} - \mathbf{r}_0) = 0
\quad\Longleftrightarrow\quad
n_x(x-x_0) + n_y(y-y_0) + n_z(z-z_0)=0.
$$
거리·면적·체적 계산 기초
점–평면 거리
점 $P(x_1,y_1,z_1)$에서 평면 $\mathbf{n}\cdot(\mathbf{r}-\mathbf{r}_0)=0$까지 거리
$$
d = \frac{|\mathbf{n}\cdot(\mathbf{OP}-\mathbf{r}_0)|}{|\mathbf{n}|}.
$$
두 직선 사이 거리
평행하지 않은 두 직선이 방향벡터
$ \mathbf{d}_1,\mathbf{d}_2 $
에 법선
$$ \mathbf{n}=\mathbf{d}_1\times\mathbf{d}_2 $$
이고 한 점간 거리
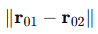
이면
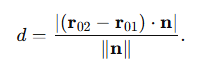
평행육면체 체적
세 벡터 $\mathbf{a},\mathbf{b},\mathbf{c}$가 이루는 평행육면체의 부피
$$
V = |\mathbf{a}\cdot(\mathbf{b}\times\mathbf{c})|.
$$
실전 문제 풀이 팁
- 좌표평면도를 그려 벡터 위치와 방향을 명확히
- 단위벡터와 성분을 활용해 방정식 수립
- 내적/외적 공식을 외워 두되, 기하 의미도 함께 기억
- 계산 실수 주의: 부호와 순서(외적은 교환법칙 불가능)
- 예각·둔각 판정: 내적의 부호로 즉시 가능
결론
공간벡터와 3차원 좌표의 기본 원리는 벡터 연산 네 가지(덧셈·스칼라배·내적·외적)와 이를 이용한 직선·평면 방정식, 거리·체적 계산에 있습니다. 이 개념을 체계적으로 익히면, 복잡한 공간 기하 문제도 벡터 한 줄로 깔끔히 정리할 수 있습니다. 오늘 정리한 공식을 바탕으로 다양한 3D 벡터 문제를 유형별로 연습해 보시기 바랍니다.
'과학 생물 천체 공학 수학 > mathematics' 카테고리의 다른 글
| 벡터를 활용한 삼각형 면적 및 사면체 체적 계산 가이드 (0) | 2025.05.18 |
|---|---|
| 직선·평면 방정식 총망라 (0) | 2025.05.16 |
| 루트 개념 정리: 제곱근, 실수, 음수 루트까지 완벽 정리 (0) | 2025.05.11 |
| 수학으로 밝혀낸 위작의 진실 (0) | 2025.05.08 |
| 경우의 수 이해법 (0) | 2025.05.06 |



